基礎医学生物学研究者のブログ

注目キーワード

用量反応関係（dose-response relationship）の測定結果をRのパッケージminpack.lmを使ってヒルの式にフィッティングしEC50を求める

日付；2025/05/8（木）

目次

はじめに

ある薬剤にして何らかの生物現象、例えば、標的分子の発現量の減少、増殖能の抑制、アポトーシスの発生率等に対する薬効を数値化し、横軸（X軸）に用量（ここではDose）、縦軸（Y軸）に反応性（ここではResponse）をとってグラフ化すると、いわゆる「シグモイドカーブ」という曲線に従うことが多い。特に、あるタンパク質に対するリガンドの結合と、結果して起こるタンパク質の反応性は、ヒルの式で表すことができる。このヒルの式から、その薬剤やリガンドのEC50（Effective Concentration at 50%）を計算することが出来る。

ウェット実験を主に行っている基礎生物学研究者や学生がこれを求めようとすると、KaleidagraphとかGraphpad Prismとかを使って、意味もよくわからず完全なブラックボックス状態でEC50を求めることが多い。職場や研究室にこのような高価なソフトウェアがあって、それを各自自由に使用出来るのであれば問題はない。しかし、いざその研究室を卒業したり、その裕福な職場を退職して、次の場所でそのようなソフトが利用出来ないような場合はどうすのだろうか。自分はそのような状況が嫌いで仕方なかった。今風にいえば、個人の能力に関するサステナビリティーが全く無い。それに、高給なソフトウェアのスネをかじってばかりでは、いい歳こいて「あのソフトの4パラメーターシグモイドカーブ」とか、なんかダッサい感じで解析することになる。そんな呼び方でしっかりした論文とか、研究とか出来ない。そしてそんな能力のヤツやラボは最終的に微妙なことになるに決まってる。だって、サステナビリティーが無いのだから。自分はこのサステナビリティー問題に修士くらいに気がついていたので、そのころからRを使っている。いまからかれこれ15年以上も前になってしまうが、そのころはまだ研究をRで使用することに対してコンセンサスがあまり得られていなかった。しかし、今は全く逆である。「は？Rでやれや。」である。

ということで、ここではRパッケージであるminpack.lmを使ったヒルの式へのフィッティング方法を述べる。このminpack.lmというパッケージはレーベンバーグ・マルカート（Levenberg-Marquardt；LM）法という非線形回帰のアルゴリズムを使っている。この方法だと、ヒルの式に限らず様々な式に対して実験で得られた結果をフィッティングできる。自分は過去に、放射線生物学分野でのLQモデル（Linear Quadratic model）やその派生モデル、マウス腫瘍モデルへの一般的なシグモイド曲線のフィッティングで使用してきた。そして、最近では創薬の分野で仕事をしており、いざとなったときにこの辺りをパッと計算でき、コストもなく、統計的にも必要最低限は計算できるという状態である。いうても、その研究室や職場でSOP（Standard Operating Procedure）が定まっている場合はそれに従わなければならないが、それが明確でないのならば、Rでちゃんと計算した方が良いと思う。

使用するデータ

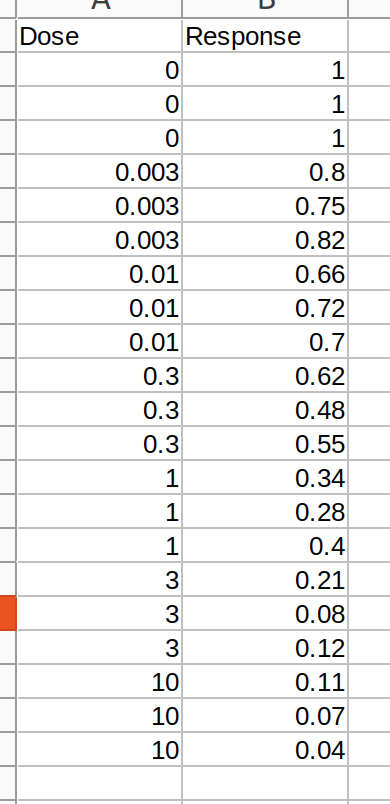
ここでは以下の画像のようなデータを使用する。Doseで示される薬剤濃度でとある薬剤を入れ、その濃度に対する薬剤の標的タンパク質の発現量を測定し、それをDoseが0の場合を1に正規化、つまり、Doseが0の場合の測定値で、各濃度を入れた場合の値をResponseとしたデータである。ちなみに、これが教科書的に言えばp/1-pの値である。実験は3回繰り返しているので、各数字が3回ずつ繰り返されている。

使用するライブラリ

ライブラリとしては以下を用いる。LM法を使うためのminpack.lm、データを整形するためのtidyverse、結果のエクセルを読み込むためのreadxlを使う。

書いていて気がついたのだが、tidyverse使わんかったわ。このような数字データだとどうしてもtidyverseよりも、2個目のコードチャンクにあるようなoriginal[original$Dose != 0,]の方が良い。

R
library(minpack.lm)
library(tidyverse)
library(readxl)
R

データを読み込む

データを読み込まなければ話は始まらないので、read_xlsx()を使って、測定値を読み込む。これは、一番最初にあったエクセルのデータである。読み込んだデータをoriginalとする。

次に、Doseが0の場合の値を削除する。そもそも、loog(0)が可視化出来ないし、さらにはp/1-pやlog(p/1-p)の計算できないためである。ということは、万が一通常のロジスティック回帰log(p/1-p) = a+b1x1+b2x2…..を行わないと行けない場合、それが計算できない。

R
# "/path/to/your/result/dose_response.xlsx" をdose_response.xlsxを保存しているディレクトリに変える。
original <- read_xlsx("/path/to/your/result/dose_response.xlsx")
analysis <- original[original$Dose != 0,]
R

初期値を設定する

次に、ヒルの式のパラメーター計算するための初期値を設定する。ヒルの式は、この論文の式（https://www.sciencedirect.com/science/article/pii/S1056871914002470）を使用する。おそらく、IGORでもKaleidagparhでもGraphpad Prismでも同じような式を見ることが出来ると思うので、ラボで普段使用している方を使えば良いと思う。というか、うちの職場もGraphpad Prism使ってるんだから、それを使えば良かった。でも、数式に論文を引用できるなら、そっちの方が良いか。

R
dose_half <- (analysis[analysis$Response == min(analysis$Response),]$Response + analysis[analysis$Response == max(analysis$Response),]$Response)/2

parStart = c(base=analysis[analysis$Response == min(analysis$Response),]$Response,
             max=analysis[analysis$Response == max(analysis$Response),]$Response,
             dose_half=dose_half,
             rate=1)
R

ヒルの式を定義する

以下がヒルの式である。これはminpack.lmの公式マニュアルにあるexample 1をそのままパクったものである。まずは、ヒルの式（ここでは関数名をhill()とする）と残渣を計算する関数（ここではresidFun()とする）を定義する。

R
# Hill equation
hill <- function(dose, base, max, dose_half, rate) {
  base + (max - base) / (1 + (dose_half / dose)^rate)
}
# Residual function
residFun <- function(par, dose, observed) {
  base <- par["base"]
  max <- par["max"]
  dose_half <- par["dose_half"]
  rate <- par["rate"]
  observed - hill(dose, base, max, dose_half, rate)
}
R

minpack.lmパッケージのnls.lm()によりフィッティングする

そして次に、フィッティングする。これにより、与えられた関数の平方和を最小にするようにパラメータが決まる。すなわち、ここではヒルの式へのフィッティングによって得られた、生存率などの値の推定値と、実際の実験により得られた生存率の差を最小にするようなパラメーターを見つけに行く。

R
nls.out_analysis <- nls.lm(
  par = parStart,
  fn = residFun,
  observed = analysis$Response,
  dose = analysis$Dose
)

# stats
summary(nls.out_analysis)
R

フィッティングを評価する

結果の統計をみるためには、summary()を使えば良い。

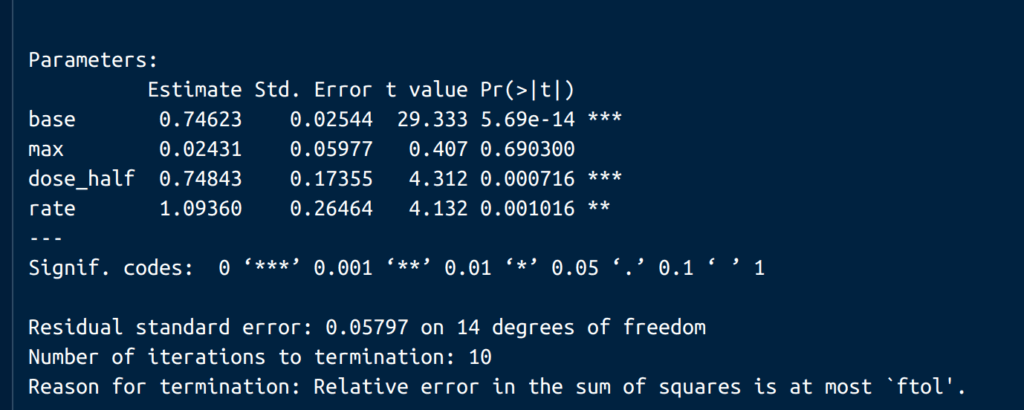
次にちゃんとモデル式（ヒルの式）にフィットしているかどうかを判断するために、R2乗を計算する。まずは求めたパラメーターが無いことにはどうしようもないので、独立変数（analysisデータフレームのDose変数）と一致する値に対する予測値（estimate変数とする）をanalysisデータフレームに入れる。

R
# Hill equation
# hill(dose, base, max, dose_half, rate) 

nls.out_analysis$par[1] # base
nls.out_analysis$par[2] # max
nls.out_analysis$par[3] # dose_half
nls.out_analysis$par[4] # rate

for(i in 1:nrow(analysis)){analysis$estimate[i] <- hill(analysis$Dose[i],
                                                    nls.out_analysis$par[1],
                                                    nls.out_analysis$par[2],
                                                    nls.out_analysis$par[3],
                                                    nls.out_analysis$par[4])}
R

次に、残渣の平方和（RSS）と、総平方和（TSS）を求めて、それらよりR二乗を求める。残渣の平方和が、各Doseにおける推定値と実測値がどれだけずれているか、総平方和が、各Doseにおける実測値と推定値の平均値とのずれ、すなわち、推定値に対する実測値のばらつきである。この2つを使ってR二乗を求める。このminpack.lm()の欠点はここで、一発でR二乗まで計算してくれないところである。

R
# Calculate Residual Sum of Squares (RSS)
rss <- sum((analysis$Response - analysis$estimate)^2)

# Calculate Total Sum of Squares (TSS)
tss <- sum((analysis$Response - mean(analysis$estimate))^2)

# Calculate R^2
r_squared <- 1 - (rss / tss)

# Print R^2
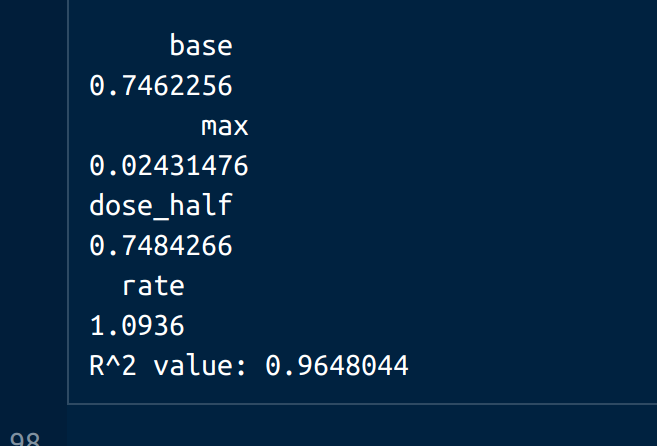
cat("R^2 value:", r_squared, "\n")
R

R二乗が0.9648044でフィッティング出来た。また、EC50の値は0.7484266らしい。

EC50の値は0.7484266、R2乗は0.9648044らしい。

ggplot2で図示する

次に、フィッティングにより求めた推定値を、実測値のドットプロットに載せることにする。そのためにはggplot2を使う。こっちのほうがグラフがキレイだろうから。まずは1000000刻みで0.003から10までのDoseという変数を持つanalysis_estimateというデータフレームを作成し、上記までに求めたヒルの式に入れてestimateという変数を作る。なぜこんなにDoseつまり、作成しようとする図のX軸をこんなに細かく刻むかと言えば、なめらかな曲線にしたいからである。ということで、ここで作成したanalysis_estimateというデータフレームは、求めたい曲線用である。

R
# data frame for predected values.
analysis_estimate <- data.frame(Dose = seq(0.003, 10, length.out = 1000000))
analysis_estimate$estimate <- hill(analysis_estimate$Dose,
                                 nls.out_analysis$par[1],
                                 nls.out_analysis$par[2],
                                 nls.out_analysis$par[3],
                                 nls.out_analysis$par[4])
R

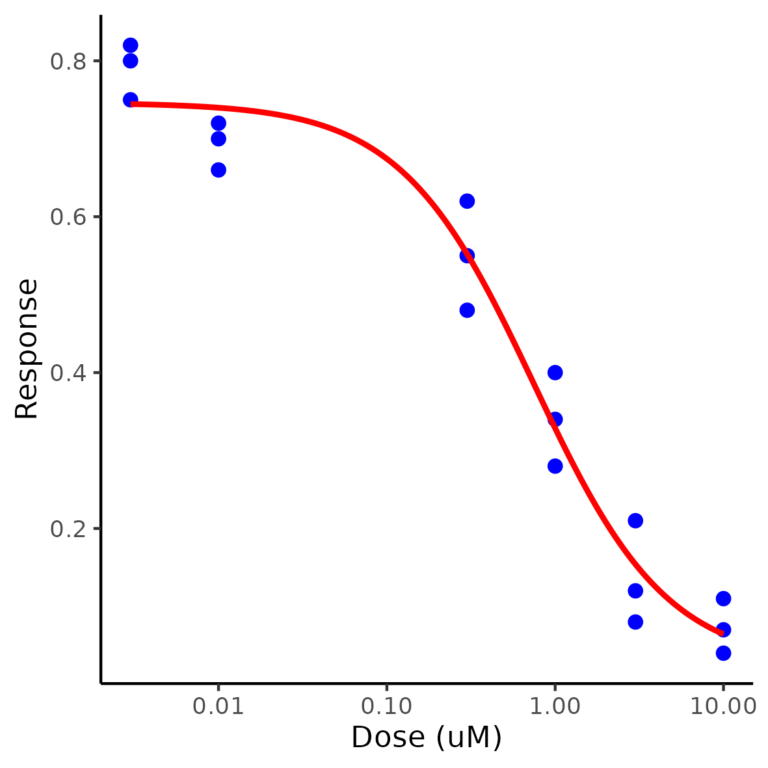
次に、実測値をドット（ポイント）に、analysis_estimateの推定値を曲線にしてプロットする。もし必要ならば、ggsave()で直前の出力を保存することが出来る。

R
# plot
ggplot() +
  geom_point(data = analysis, aes(x = Dose, y = Response), color = "blue", size = 2) +
  geom_line(data = analysis_estimate, aes(x = Dose, y = estimate), color = "red", size = 1) +
  scale_x_log10(limits = c(0.003, 10)) +
  labs(
    x = "Dose (uM)",
    y = "Response") +
  theme_classic() +
  theme(
    plot.title = element_text(hjust = 0.5)
  )
# ggsave("path/to/your/plot.png", width = 10, height = 10, units = "cm")
R

これを流せば、以下のようなグラフが出力される。

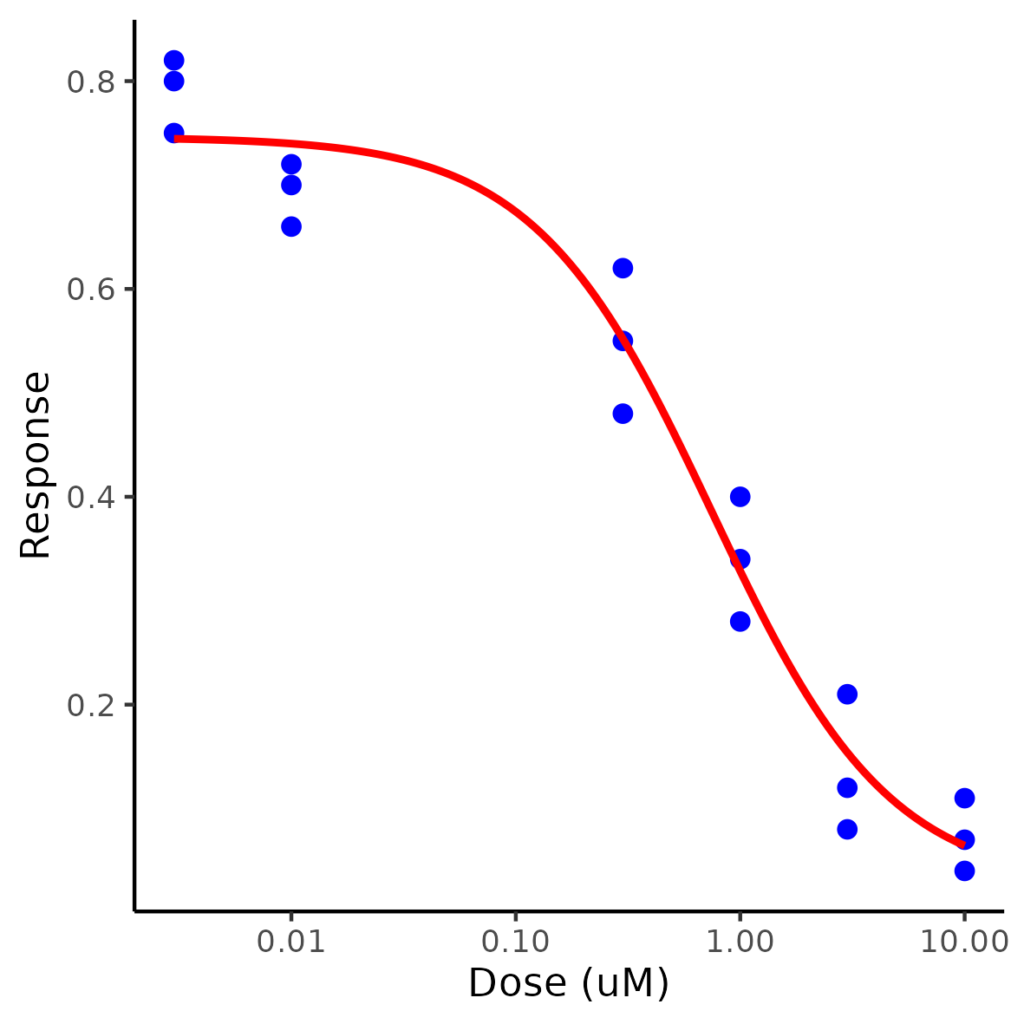
まとめ

これで、薬理試験におけるEC50をRで求めることができる。正直、これよりもフィッティングの結果が良いソフトはGnuplotがある。もしminpakc.lm()を使っていてなんかフィッティング結果が悪いなってときは、このminpack.lm()で求めたパラメータを初期値にして、gnuplotで求めたら良い。SASのPROC NLIN Method = MARQUARDTでも似たようなことが出来る。だたし、これは求めたいパラメーターで偏微分した式が必要だった気がする。最近はSAS OnDemand for Academicsというフリー版もあるので、アカデミックの人は試したら良いと思う。自分はGnuplotが一番好きである。同じアルゴリズム使っているのに、なぜかGnuplotは結果が良い気がする。

「はじめに」でも述べたが、フィッティングに他のモデル式を使いたい場合、hillの式の定義のところを別の関数に置き換えて、その後に設定・取得するパラメーターも適宜変えれば、それでもうまいことフィッティング出来る。マウス腫瘍をそのシンジェニックマウスに移植した場合の腫瘍増殖曲線なんかは一般的なシグモイドカーブで良くフィットするし、放射線生物のLQ（Linear Quadratic）モデル、その派生モデルなんかもうまいことフィットできる。